➗ Standard deviation
When we speak in statistics of the standard deviation or the standard deviation, it is represented by the Greek letter Sigma σ (in lowercase), as well as by the Latin letter (s) or by its acronym in English SD (Standard Deviation) and is a measure A that quantifies the spread or variation of a data set.
When we have a decreased standard deviation, this implies that most of our data from the sample are grouped very close to the “expected value”, that is, its mean. If, on the other hand, we have a high standard deviation, this tells us that our data is extended over a more extended range of values.
It is important to note that the median is calculated by adding all the data we have and dividing it by the number of data.
General considerations
When we refer to the standard deviation of some statistical population, random variable, probability distribution or data set, we can find it with the square root of its variance.
But what if we ask ourselves what is the variance? Variance is the measure of dispersion that exists between a random variable, but with respect to its mean value. It must be understood that this is nothing more than the mathematical expectation and to find it we must first square the difference between the variable and what is expected of it.
While it is true that this is algebraically much simpler, in practice the standard deviation can be considered to be less robust than the mean deviation. However, a standard deviation has a very useful property and that is that it can be expressed in the same units as the data from which that standard deviation came and also expresses the variability that a population has.
On the other hand, the standard deviation is also used to measure the reliability of our statistical conclusions. For example, when we refer to opinion polls, we can calculate the margin of error that our data has, through the standard deviation of the results, of course, to achieve this, the survey must be repeated several times.
This type of interpretation of the standard deviation is what is called “the standard error” of the estimate and when it refers to a statistical median, it is called “the standard error of the mean”. So we can calculate all the means of a population from which we can extract an infinite number of samples, to later calculate the mean for each of those samples and then obtain our standard deviation through the formula.
You should be aware that the standard deviation obtained from a population and its standard error (such as the mean) are very different, but are related by a factor, which is the inverse of the root of the number of data taken from the sample. . Now, the margin of error that any survey has, can be calculated by means of the standard error that its mean has. But you can also calculate the margin of error, such as the product that exists between the standard deviation that the population has, by the inverse of the square root of the amount of data that is represented in the sample (it is the same).
Generally, if we take a 95% confidence interval, half its width will be approximately equal to twice the standard deviation.
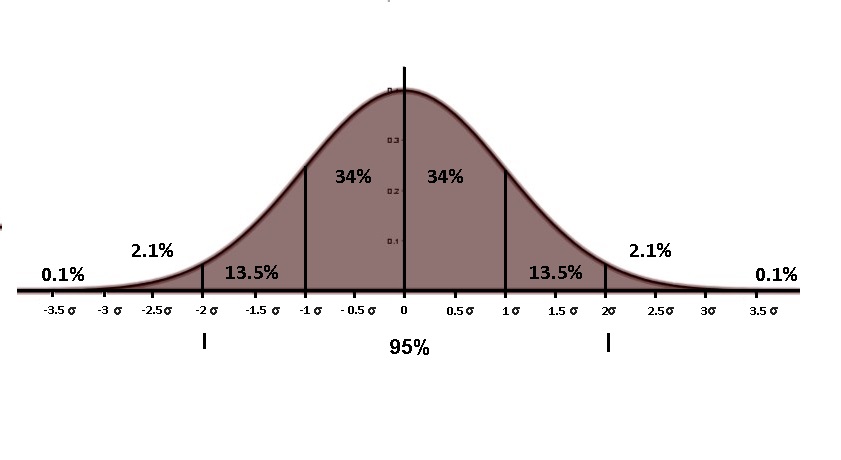
Many scientific researchers consider the standard deviation from experimental data, and only those effects that are twice the standard deviation away from what they consider to be “expected” are what researchers can consider statistically significant. This is how they distinguish common variation in measurements, or normal random error, from truly genuine and significant effects.
When it comes to finance, the standard deviation is also an important indicator, since the rate of return on any investment uses this deviation to give you an idea of its volatility. Suppose we have at our disposal a sample of data from some population of our interest, the sample standard deviation or standard deviation of the sample, can refer to twice what is known as the standard deviation applied to these data or it can also be a amount to which an adjustment is made to serve as an unbiased estimate of the much-referred standard deviation applied to the entire population.
Let’s go with an example to clarify the above:
A math teacher after an exam obtained the following results:

04, 17, 09, 10, 12, 05, 15, 14, 11, 10
The teacher considers that the range of the points obtained in his last test is very large. What would the range be?
You have indicated that if the mean deviation of the test is greater than 4, you will repeat the test. Will the students take the test again?
The class teacher has pointed out that if he obtains a variance of 7, the results would be favorable. What would the variance be?
You also decide that depending on twice the standard deviation, you will repeat the test. Given the case that 2 σ> 6 will propose to carry out another exam, will this be the case?
The first thing I have to do is order my data from smallest to largest:
04, 05, 09, 10, 10, 11, 12, 14, 15, 17
As we know, the variance measures the dispersion of the data representing the variable, but with respect to the arithmetic mean, so the greater the variance, the greater the difference between the data and the mean, that is, the greater the variability. If the teacher assumes that a variance of 7 is favorable, we can deduce that a variance of 15.21 will be unfavorable.