🥇 Fibonacci series
The Fibonacci series, the golden ratio, and how they describe the universal proportions of the world around us
Leonardo de Pisa was an Italian mathematician who is better known throughout the world as Fibonacci. This mathematician discovered a sequence commonly known as “The Fibonacci series”; he came up with this idea when calculating the number of rabbits that could be bred over a period of several months.
Suppose that at the beginning of the first month we have a pair of newborn rabbits. Therefore, we have one (1) pair of rabbits that will take a month to develop enough to be able to mate. So at the end of the first month, we mate this pair of rabbits and, adding together the number of pairs in this generation and the previous generation, we have 1 + 0 = 1 couple—the same pair of rabbits, because the babies have not yet been born.
Now, at the end of the second month the first couple gives birth to a second pair of rabbits and then mates again. The newborn pair is (of course) not yet matured and the next pair of babies has not yet been born, so we have 1 + 1 = 2 pairs of rabbits.
By the end of the third month, the first pair of rabbits gives birth to a third pair and mates again. The second pair is now mature and mates. The first pair has already sired two pairs of rabbits, but neither of these pairs has sired any of their own children yet. Two pairs—the ones from one month ago—survive into this generation, but only one pair—the one from two months ago—is old enough to birth a new pair for this generation. Therefore, the number of pairs for this month is: 2 + 1 = 3
At the end of the fourth month, the first pair of rabbits has sired three pairs, while the second pair has sired their first pair of rabbits. So we have one pair for each of the rabbits in the previous month, 3, plus one extra pair for each of the pairs two months ago, 2, because only those pairs are old enough to produce children for this generation. This gives 3 + 2 = 5 pairs of rabbits this month.
If we keep doing these calculations from the starting point of 0 and 1, adding the previous two numbers together, we can continue the sequence:
0 + 1 = 1
1 + 1 = 2
1 + 2 = 3
2 + 3 = 5
5 + 3 = 8
8 + 5 = 13
13 + 8 = 21 and so on

The Fibonacci sequence in nature
This type of mathematical pattern is found in countless places within nature. For example, the number of petals a flower has almost always matches a number in the Fibonacci series. Some flowers have 3 petals, you will find others that have 5 petals, some will have 8, and you can even find flowers with 13 petals. Much less often will you find a flower with a number of petals that does not match a Fibonacci number. That is, with 4, 6, 7, 9, 10 or 11 petals.
The numbers that belong to this series are presented in a big part of the world that surround us.
In the year 1753 a Scottish mathematician named Robert Simson discovered that the quotient of two consecutive numbers in the Fibonacci series tends towards 1.6180339… as the numbers get larger. The result will always be alternatively somewhat above or somewhat below 1.6180339… but trends closer and closer without reaching it absolutely.
The number to which the relationship between two successive numbers of this same series converges is called the golden ratio. It is an irrational number, like the more well-known irrational numbers pi and e, and is denoted by the Greek letter phi.
If you closely track the angular positions of the seeds of a sunflower as they spiral out from the center, you may notice that each seed is at a certain fixed angle from the one next closest to the center, and that this angle is approximately 137.5º. This is called the golden angle, and it is obtained by partitioning the 360º degrees of a circle into two parts according to the golden ratio.
This angle allows the seeds to pack into the space available in the most optimal way, that is, with the least leftover space. This causes the seeds or florets to completely cover the disk of the sunflower in a characteristic spiral pattern. This angle allows the new leaves that are generated in the sunflower to not block the sun for the previous leaves and also cover the maximum amount of surface, thus receiving as much sun as possible. The same phenomenon occurs with the leaves of an artichoke.
But it does not end there. If you count the spirals that form in the center of a sunflower, you will realize that there are 89 spirals in one direction and 55 in the other; they can also have 144 and 89. Both are successive pairs from the same illustrious sequence.
Trees do not escape this phenomenon. If you look closely at the angle that is formed between two consecutive branches, you may realize that they too have an angle of approximately 137.5º between them.
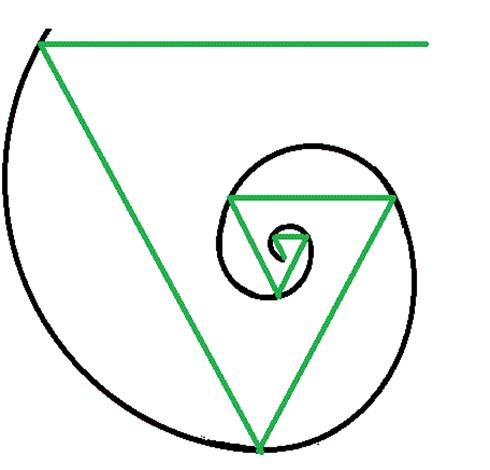
The sequence discovered by Leonardo de Pisa is also related to the so-called golden spiral, which is generated by drawing a series of adjacent squares, the sides of which are made up of the terms of the Fibonacci series. The spiral is formed by combining quarter-circle arcs with radii equal to the side lengths of these squares.
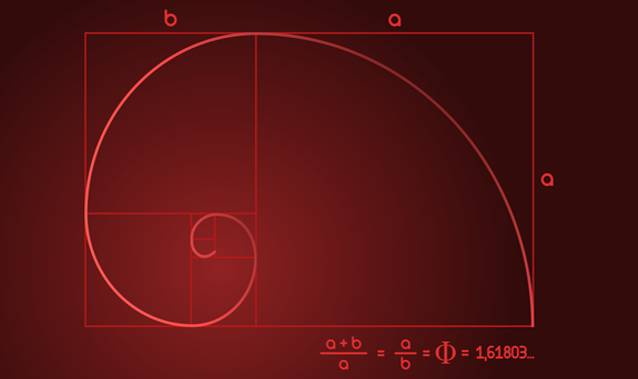
The shell of a nautilus (a type of cephalopod mollusk) has a similarity with the golden spiral, only that instead of be formed with arcs through the sides of squares, it is formed with arcs through the sides of equilateral triangles. For a given fixed side length of the starting polygon, Fibonacci spirals formed from triangles spiral in more tightly than those formed from squares.

Not satisfied with the similarities described above? We also see that equivalent spirals are present in certain galaxies and hurricanes.


The Fibonacci series and the golden ratio in art
Great composers of the 20th century, such as Olivier Messiaen, Delia Derbyshire, Béla Bartók, and the band Tool, used this famous succession to invent new musical structures and to inspire their art.
The golden ratio, phi, has been directly involved in art for thousands of years, and was associated with the ideal proportions of certain ancient architectural structures.
This importance of the golden ratio in art and architecture may be related to this special construction: If one divides a distance into two unequal segments, such that the ratio of the lengths of the longer segment and the shorter segment is equal to the ratio of the lengths of the entire distance and the longer segment, these ratios will be equal to the golden ratio.
That is to say:
a / b = (a + b) / a
Where “a” is the longer segment and “b” the shorter.
The Pyramid of Giza has a length of 230 meters on each side of its base and its height is 146 meters. The relationship between the two measures is approximately 1.575, which is quite close to the golden ratio of 1.618.
A rectangle whose length and width satisfy the golden ratio is called a golden rectangle, and is considered one of the most visually satisfying geometric shapes.
Even the famous mathematician and sculptor Phidias, born in 500 BC, is believed to have applied the golden ratio to the design of sculptures in the Parthenon.
The Franciscan friar, economist, and mathematician Luca Bartolomeo de Pacioli was highly recognized for being one of the early contributors to the field of accounting and inventor of double-entry book-keeping. He published a mathematical treatise in 1509 called “De divina proportione”, which was illustrated by none other than Leonardo da Vinci. He claimed that “without mathematics there is no art” and intended to reveal the mathematical secrets of harmonious forms to the artists of the time with this treatise, using the golden ratio as his main tool.
Leonardo da Vinci himself, through what he called the “sectio aurea”, or “golden ratio”, exhibited the ideal symmetry in his paintings “The Mona Lisa”, “The Last Supper”, and “The Vitruvian Man”.
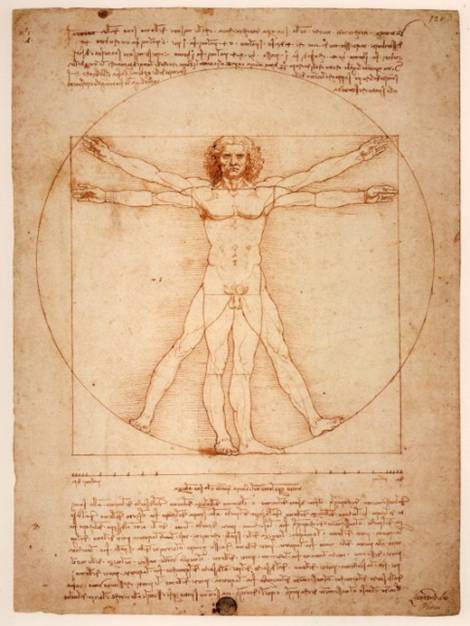
Da Vinci claimed a relationship between ideal human proportions and the golden ratio. He observed that the ratio between height and the distance from the ground to the navel approached phi for particularly harmonious figures. Similarly, the ratio of the distance between the fingers and the shoulder and the distance from the elbow to the fingers seemed also to approach this number. “The Vitruvian Man” was designed with these ideal proportions.
As if that weren’t enough, this sequence has multiple applications in mathematics, computer science, and game theory. As one example, take this mathematical curiosity: add any ten consecutive numbers from this famous series, and the result will always be a multiple of 11. Clearly, the Fibonacci series is at the center of countless fascinating mathematical anecdotes.